2021-10-28 17:18:20 辽宁华图公考问答 http://ln.huatu.com/wenda/ 文章来源:云南分院
阜新华图_辽宁公务员考试网为您提供备考文章:2022国家公务员备考行测之积定增减模型。欲了解公务员招聘信息敬请关注阜新华图公务员招聘频道(http://fuxin.huatu.com/)或者关注阜新华图微信公众号(fuxinht),阜新华图咨询电话:0418-660996。
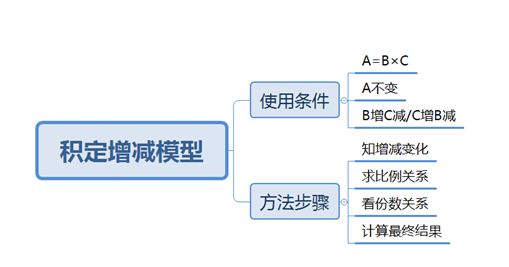
不管是在公务员还是事业单位考试中,数量关系形如“A=B*C”形式的题型非常常见,比如:路程=速度X时间;总量=平均数X个数;体积=底面积X高;总量=时间X效率;面积=长X宽……针对此类问题,大部分考生都习惯用方程法求解,虽然方程法也可以得出结果,但是列式及其计算过程过于繁杂,而考试时间有限。所以,华图教育在此给大家介绍积定增减模型在此类题型中的运用。
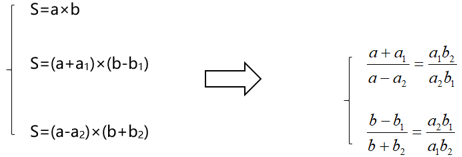
在此,我们首先以大家最熟悉的长方形的面积公式着手讲解其推导过程:
【例】假设长方形面积为s,长为a,宽为b;如果长增加a1,宽减少b1;如果长减少a2,宽增加b2,那么长和宽的变化情况如下表:
长和宽的变化情况
| 变化的长 | 变化的宽 |
+a1 |
-b1 |
-a2 |
+b2 |

![]()
通过长和宽的变化情况,根据面积不变,用对角线相乘做比,得到的就是两次长之比;反之就是两次宽之比。得出比例之后,根据长和宽前后增加多少就可以求出原先的长和宽,进而算出面积。
推导过程如下图:
![]()
我们利用此处推论针对此类题型进行总结:①这类题型往往存在形如“”形式,且“A”不变,而“B”和“C”存在增减关系(B增C减/C增B减)。②此处得到的两个比例一个为两次新长度之比,对应为“第一次与第二次长度变化比乘以第二次与第一次宽度变化比”;一个为两次新宽度之比,由于面积不变,所以刚好与新长度之比成反比。③涉及到变化量“a1、a2、b1、b2”等,不考虑增减,看绝对值即可。
为了便于大家理解,这里提供几个经典例题:
【例1】小杨开车从老家回单位,若速度增长10千米/小时,则提前30分钟到达;若速度减少8千米/小时,则推迟30分钟抵达。那么小杨家离单位多少千米?
A. 288
B. 360
C. 405
D. 450
【解析】第一步,本题考查行程问题,属于基本行程问题。
![]()
第二步,本题涉及“”形式,且“A”不变,而“B”和“C”存在增减关系。由于30分钟=0.5小时,第一个速度、时间变化量分别为10和0.5,第二个速度、时间变化量分比为8和0.5;所以新速度之比=,新速度一个“增加10”,一个“减少8”,二者相差18,可得第一个速度5x18=90,第二个速度4x18=72。同理,新时间之比为,新时间一个“提前0.5小时”,一个“推迟0.5小时”,二者相差1,可得第一个速度4x1=4,第二个速度5x1=5。即全程等于90x4或者72x5,均为360千米。
因此,选择B选项。
【例2】单位端午节发放福利卡,如果增加3名员工,则每人少分8张;如果再增加4名员工,则每人再少分8张。那么福利卡共有几张?
A. 672
B. 1344
C. 2016
D. 2688
【解析】第一步,本题考查基础应用题。
![]()
第二步,本题涉及“”形式,且“A”不变,而“B”和“C”存在增减关系。
![]()
由于第一次人数、人均张数变化量分别为3和8,第二次人数、人均张数变化量分比为7和16;所以两次人数之比=,两次人数一个“增加3”,一个“再增加4”,二者相差4,可得第一次人数6x4=24,第二次人数7x4=28。同理,两次人均张数之比为,人均张数一个“少分8张”,一个“再少分8张”,二者相差8,可得第一次人均张数7x8=56,第二次人均张数6x8=48。即总数等于24x56或者28x48,均为1344张。
因此,选择B选项。
【例3】一个长方形面积不变,如果长增加10米,宽减少8米;如果长减少5米,宽增加12米。那么该长方形面积多少平方米?
A. 175
B. 200
C. 225
D. 250
【解析】第一步,本题考查几何问题,属于基本公式型。
![]()
第二步,本题涉及“”形式,且“A”不变,而“B”和“C”存在增减关系。
![]()
由于第一个长、宽的变化量分别为10和8,第二个长、宽的变化量分比为5和12;所以新长度之比=,新长度一个“增加10”,一个“减少5”,二者相差15,可得第一个长为。同理,新宽度之比为,新宽度一个“减少8”,一个“增加12”,二者相差20,可得第一个宽为1x10=10,第二个宽为3x10=30。面积等于,均为225平方米。
因此,选择C选项。
![]()
通过这些题目,我们不难看出,无论题目形式如何多变,但是内涵本质不变。在备考阶段遇到这类题型形如“”形式,且“A”不变,而“B”和“C”存在增减关系。可直接采用积定增减模型的方法步骤做题,缩短做题的时间,提高做题效率。
(编辑:阜新华图01)

贴心微信客服

贴心QQ客服
下一篇:没有了